-
ホーム
-
SPI非言語
非言語分野(数学)の特徴
能力検査の非言語分野(数学)では言語や語彙についての主に数学の問題が出題されます。
出題傾向について、大きく分けて以下の9つに分類できます。
①推論
②表の読み取り
③集合
④場合の数
⑤確率
⑥金額計算
⑦分担計算
⑧速度算
⑨割合
上記の分野から出題されます。
基本的に、中学・高校で習う数学の基礎問題から出題される傾向があります。
そのため、全体的に難易度が高い問題が出題される訳ではないのですが、数学の分野のため
公式や解き方を理解していないと解答できない問題がほとんどなため、対策せずにSPI試験に臨むのは避けた方が良いでしょう。
また、先ほど述べた9つの分野から試験が出題されるため、試験範囲が幅広く全ての分野を幅広く抜かりなく対策する必要があります。
その為、短期で勉強をするよりも、時間をかけてSPI試験の対策に取り組み、苦手分野の克服に努めるのをおススメします。
実際、SPI非言語分野の試験について「解答時間が短く、問題数が多い」という特徴があります。
SPI試験の実施方法によっても出題数や制限時間は変わるものの、基本的には30分程度の制限時間で約30問の問題を解答する必要があるため、1問につき1分で解答をする必要があります。
その為、基本的には公式を思い出して解答をするというよりも、直感的に解答をするためのスピードと正確性が求められます。
難しい問題が出題された場合には、問題を飛ばす事も覚えておきましょう。
以下に先程あげた、各項目の例題と、解説を記載します。
ぜひSPI試験対策の参考にしてください。
「推論」問題の概要
推論も問題では、試験の設問内で与えられた情報やグラフを読み取り、定められた数値を計算し求める問題です。
推論の問題の中でも、大きく分けて7つの出題形式に分けることができます。
⑴順序:設問で与えられた情報やグラフから正しい順番を計算する問題
⑵密度:設問で与えられた情報やグラフから人口密度などを計算する問題
⑶発言の正誤:複数人の発言から、会話内の矛盾を見つける問題
⑷対戦:設問で与えられた情報やグラフから試合結果などの勝敗の結果を計算する問題
⑸位置:設問で与えられた情報やグラフから位置関係を計算する問題
⑹平均:それぞれの情報から、平均値を求める問題
⑺内訳:情報から個数や人数などの詳細を解答する問題
上記の7つは必須で出題されるといっても過言ではないので、計算するための公式・解き方をしっかりと勉強しておきましょう。
推論の勉強方法として、SPI問題集を繰り返し解くことや、SPIの模擬試験を受験することが挙げられますが、「文章をグラフや表に落とし込み情報を整理すること」と「考えられる可能性を全て書き出すこと」の2つがポイントです。
1問につき1分という限られたじかんの中で、いかに情報を偽りなく正確に把握し、求められている数字を算出できるのか?を確認できるように慣れてください。
「表の読み取り問題」の概要
表の読み取り問題では、文字通り、表やグラフを読み取って計算する問題です。
表の読み取り問題に関して、4つの分野に分けることができます。
⑴数量の表:表やグラフを用いて数量や物の割合などを求める問題
⑵割合の表:表やグラフから、割合を求める問題
⑶2つの表:2つの表から数量と割合を求める問題
⑷特典範囲の表:グラフから、平均点や中央値などを求める問題
こちらの問題ではいかにグラフを正確に読み取り、どの数字を計算に用いるのかを素早く把握することがポイントになります。
基本的には、増加数・減少数という具体的な数字と、何%増加・減少したのかを算出することがことが多いため、解き方や計算方法を見直しましょう。
問題によっては、グラフから複数の数字を計算し、さらに計算した数字を使って答えを求める問題もあるので、チェックしておきましょう。
「集合」問題の概要
集合の問題では、設問に記されてた情報から、問題文に指定された条件に当てはまる人数を導き出す問題です。
この問題では、情報を見てどの数字がどの属性を持っているかをグラフに落とし込むことで見える化することで正答率がググッと上がります。
よくグラフ化する中で用いられるのが「ベン図」と「カルノー」図です。
それぞれ、「カルノー図」では2つの項目について整理したい時に用いるのが便利で、
「ベン図」に関しては、3つ以上の項目を整理したい時に適しています。
そのため、基本的には「ベン図」を用いて整理することができるように準備しておくことが重要です。
「場合の数」問題の概要
場合の数は、何通りの組み合わせ・並び方があるかを導き出す問題です。
よく、先程あげた「推論」分野の「順列」問題と同じように考えている方がいますが、大きな違いは、順番を考えた解答をするかどうかになります。
こちらの問題の解答のポイントはとにかく公式を覚え、計算になれることです。
特に、「順列の公式」・「組み合わせの公式」・「円順列の公式」の3つは必須級なので考えなくてもすぐに計算に取り組めるようになるまで、繰り返し対策をしましょう。
「並べる」・「列」という文言や「選ぶ」・「組み合わせ」などといったキーワードが、問題文に記載されていることも多いため、答えを導き出すために、どの公式を使うのか?覚えておきましょう
「確率」問題の概要
確率の問題では、「サイコロ」・「コイン」などを用いて問題が出題されます。
〇〇が出る確率を求める問題などが主です。
確率の問題については、苦手意識を持っている人が多い印象ですが、公式を覚えておくことで、確実に点数を取れる問題でもあります。
確率の問題はほぼ確実に出題される分野の為、確率の問題でも先程の場合の数と同様に計算するための公式を覚えることが必須です。
「金額計算」問題の概要
金額計算の問題では、基本的に「割引」の問題と「損益」を計算する2つに分けられます。
まず「割引」問題では、割引きをする人の条件などが設問に記載されている事もあるため、どういう条件であれば割引をするのか?を理解し、割引する人としない人を分けて考える必要があります。
続いて「損益」を求める問題では、利益を求める問題のため、問題文から「仕入れ」「定価(原価)」「売値」などの複数の情報を拾う必要があります。
基本的に、計算方法だけ覚えておけば対応は可能ですが、中には問題文の語句がわからないという人もいると思います。
出題されそうな内容や用語を理解するようにしましょう。
「分担計算」問題の概要
分担計算では、主に「分割」と「仕事算」の2つに分けることができます。
「分割」では、金額を分割にして支払う際の手数料や利子などが付いた際の合計金額や、1回あたりの支払い金額を求める問題が主に出題されます。
割合は、基本的に分数で記載されるため、分数の計算方法について、復習しておくと良いです。
続いて、「仕事算」では仕事にかかる時間を求める問題です。
分数・割合などを用いて解答をするため、基本的には基礎を復習し解き方がわかっていれば問題なく回答ができると考えます。
「速度算」問題の概要
速度算では、「速度」「距離」「時間」の三つの情報を軸に、平均速度や追い越し時間・追いつく時間を求める問題です。
この問題では、基本的に1つの公式さえ、覚えていれば対応することが可能なため、他のSPIの問題と比べ、対策は容易であります。
一方で、計算や回答をするにあたり、単位を統一させる必要があるため、勿体無いミスが多くなってしまう問題でもあります。
SPIの問題集で練習したさいには、気をつけてください。
「割合」問題の概要
割合の問題では、条件に当てはまる数字が全体の何%かを導く問題です。
こちらの問題は、基本的な公式はなく、基本的には、足し算・引き算・掛け算・割り算といった四則計算が主にて計算を行うため、出題の傾向を把握し、練習するだけで解答をすることは容易です。
そのため、いかに早く正確に解答を導き出すかを重視して動くのも良いでしょう。
各分野の例題と解説
先程、概要をお伝えした内容について、以下に問題と解説を記載するので、ぜひ参考にしてもらえると幸いです。
推論の問題
P、Q、Rの金属に含まれる不純物の質量の割合は以下の表のとおりである。ここで、金属の質量は、PとRで等しく、QはRの2倍だということがわかっている。
この時、次の推論について、正しいものをAからCの中で1つ選べ。
・QとRに含まれている不純物の質量は等しい。
P 4%
Q 8%
R 8%
選択肢:
A. 正しい
B. どちらともいえない
C. 誤り
解説を詳しく見る
PとRの金属の質量を100、Qの金属の質量を200とおく。
すると不純物の質量は、
P 100×0.04=4
Q 200×0.04=8
R 100×0.08=8
となる。
表の読み取りの問題
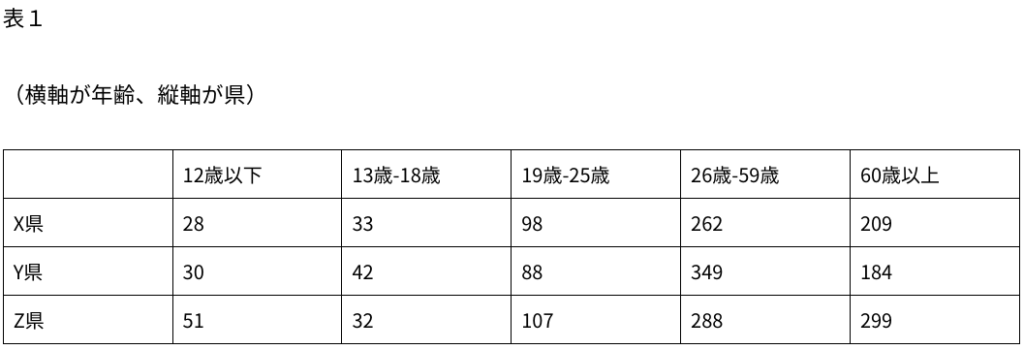
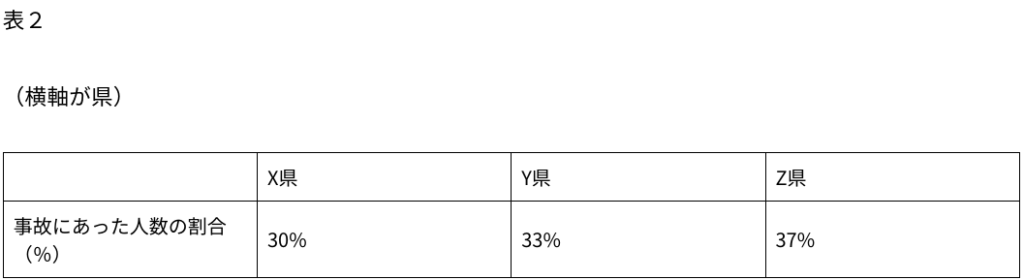
県X、Y、Zの1年間の交通事故にあった人を数えた。
表1は年齢別に人数を集計したもの、表2は県X、Y、Zにおけるそれぞれの事故にあった人の割合を示したものである。
12歳以下が事故にあった割合が最も高い県を選べ。
選択肢:
A. X
B. Y
C. Z
D. 表から読み取ることはできない
解説を詳しく見る
X県の事故にあった人数の総数は630人。うち28人が12歳以下なので、その割合は0.0444で約4.4%
Y県の事故にあった人数の総数は630÷0.3×0.33=693人。うち30人が12歳以下なので、その割合は0.0432で約4.3%
Z県の事故にあった人数の総数は630÷0.3×0.37=777人。うち51人が12歳以下なので、その割合は0.0656で約6.6%。
Z県が一番多い。
集合の問題
ある小学校5年生を対象とした体力テストがあった。生徒50人のうち、50m走で9秒未満で走ったのは24人で、立ち幅跳びで150cm以上を飛んだ子は20人いた。
50m走で9秒以上のタイムを要した生徒と立ち幅跳びで150cm未満の記録だった子の人数は50m走で9秒未満で走り、かつ立ち幅跳びで150cm以上の記録だった子の2倍の人数いたとする。50m走で9秒未満で走り、かつ立ち幅跳びで150cm以上の記録だった子の人数はいくらか。
解説を詳しく見る
50m走で9秒未満で走り、かつ立ち幅跳びで150cm以上の記録だった子の人数をx人とおく
図より24+20-x+2x = 50 が成り立つ。この方程式を解くと、x = 6となるので求めるべき人数は6人。
場合の数の問題
1、2、3、4、5、6の6つのうち3つの数字を使って整数を作る。各位の数字が異なる3けたの整数の個数はいくつか。
選択肢:
A. 24
B. 72
C. 120
D. 240
E. AからDのいずれでもない
解説を詳しく見る
6つの数字を3つの位に当てはめるから、
6P3
= 120通り。
確率の問題
XとYの2人がくじをひく。そのくじは1等賞が当たる確率が1/20、3等賞の当たる確率が1/5である。XとYのうち片方が1等賞、もう片方が3等賞を当てる,という事象が起きる確率を求めよ。
解説を詳しく見る
Xが1等賞を当てる確率が1/20, Yが3等賞を当てる確率が1/5なので、
Xが1等賞、Yが3等賞である確率は、1/20*1/5= 1/100であり、Xが3等賞、Yが1等賞である確率も同様に1/100なので、求める確率は、1/100*2= 2/100, すなわち2%となる。
金額計算の問題
ある商品の仕入れ値は1個あたり80円である。しかしまとめて仕入れる場合は割引がある。
51個目から100個目については1個70円、101個目以降は1個60円となる。
この商品を125個まとめて仕入れる場合の仕入れ総額を求めよ。
選択肢:
A. 7,500円
B. 8,500円
C. 9,000円
D. 9,500円
E. 10,000円
解説を詳しく見る
125個仕入れる商品のうち
1個目から50個目は80円/個、
51個目〜100個目の50個は70円/個、
101個目〜125個目の25個は60円/個である。
80×50+70×50+25X60
=4,000+3,500+1,500=9,000円
分担計算の問題
空のバッテリーを100%充電するのに、電源Pから充電すると2時間かかり、電源Qから充電すると2時間30分かかる。あるとき0%のバッテリーを電源Pから1時間30分充電して、その後少し使い、今度は電源Qからちょうど1時間充電したら100%になった。
途中で使ったバッテリーは何%分か。
選択肢:
A. 10%
B. 15%
C. 20%
D. 25%
解説を詳しく見る
最初に充電できた量は全体の75%である。
また2回目にQから充電した際、100%にするのに1時間かかっているため、充電した容量は60/150=40%分。つまり2回目の充電開始時点で容量は60%に減っていた。
つまり途中で使ったのは、75 – 60 = 15%分である。
速度算の問題
バス停Xとバス停Yは12kmはなれている。バス停XをバスPが8時ちょうどに出発し、XとYのちょうど中間地点でバス停Yを8時5分20秒に出発したバスQとすれ違った。各バスの速度は常に一定という条件のもとで、バスPが時速30km/時で走行する。
バスPとバスQがすれ違ったのはバスQがバス停Yを出発してから何分何秒後か。
選択肢:
A. 6分20秒後
B. 6分24秒後
C. 6分36秒後
D. 6分40秒後
解説を詳しく見る
中間地点はバス停Xから6km離れた場所にある。
バスPが6km移動するのに、必要な所要時間は6/30時間、すなわち12分とわかる。
バスQは8時5分20秒に出発したので、すれ違うのは6分40秒後。
割合の問題
空港Pからは空港Q、空港R行きの飛行機しか離陸しない。また、X社とY社の飛行機しか離陸しない。ある期間、空港Pから離陸していく飛行機を調べたところ、空港Qに向かう飛行機が60機、空港Rに向かう飛行機が120機あった。空港Qに向かう飛行機のうち55%はX社が、45%はY社が運行している。空港Pから離陸していく飛行機全体のうち60%はX社の運航である。空港Rに向かう飛行機のうちY社の運航は何%を占めるか。
選択肢:
A. 27.5%
B. 30%
C. 35%
D. 37.5%
解説を詳しく見る
空港Qに向かう飛行機のうちX社が運航するのは、
60×0.55=33機である。空港Pから離陸していく飛行機は合計で60+120=180機で、そのうち60%がX社が運航するのでその数は、180×0.6=108機である。
従って、空港Rに向かう飛行機のうちX社が運航するのは、108-33=75機である。
空港Rに向かう飛行機が120機なので、空港Rに向かう飛行機のうちY社が運航するのは、120-75=45機である。
従って、空港Rに向かう飛行機のうちY社の運航が占める割合は、45÷120=0.375で37.5%となる。
例題を解く
特殊計算012
正方形の庭に、周りに花を植えるためのスペースがある。庭の一辺の長さは5メートルで、花同士は30センチメートルの間隔を開けて植えることができる。庭の四隅にも花を植えることを考えている。この庭に何本の花を植えることができるか?
解説を詳しく見る
庭の一辺の長さが5メートルなので、庭の周りに花を植えるためのスペースは4 x 5メートル = 20メートル。
花同士の間隔が30センチメートル(0.3メートル)なので、庭に植えられる花の本数は20メートル / 0.3メートル = 66.67本。
しかし、庭の四隅にも花を植える必要があるため、実際に植えることができる花の本数は66.67本 - 4本(四隅の花)= 62.67本。
小数点以下を切り捨てて、庭に植えることができる花の本数は24本。
集合012
あるレストランのメニューには、ハンバーガー、ピザ、パスタ、サラダの4つがあります。100人のお客様に対して、以下の注文がありました。
・ハンバーガーを注文したお客様は40人でした。
・ピザを注文したお客様は30人でした。
・ハンバーガーとピザの両方を注文したお客様は10人でした。
・パスタを注文したお客様は20人でした。
・サラダを注文したお客様は15人でした。
・サラダとパスタの両方を注文したお客様は5人でした。
ハンバーガー、ピザ、パスタ、サラダのうち、どれも注文しなかったお客様は何人か。
解説を詳しく見る
ハンバーガーを注文したお客様(40人)とピザを注文したお客様(30人)の合計が70人ですが、ハンバーガーとピザの両方を注文したお客様(10人)を重複して数えているため、実際の異なるお客様の数は70人 - 10人 = 60人です。したがって、どれも注文しなかったお客様は100人 - 60人 = 40人です。














