-
ホーム
-
SPI非言語
-
グラフ・資料の読み取り
SPIのグラフ・資料の読み取りとは?
SPIのグラフ・資料の読み取りは、数々のデータが示されたグラフや表を正確に読み解き、それに関する質問に答える能力を試す問題です。
この問題タイプでは、数値の理解とデータの解釈が重要となります。
特に、割合や増加率の計算が頻出し、平均世帯人数などの特定の概念に関する問題もあります。
これらの問題を解くためには、表現されたデータを正確に把握し、それを基に論理的な推論を行うことが求められます。
グラフ・資料の読み取りの問題
比較と割合の計算
例えば、特定のグループ間での比較や、全体に対する割合を求める問題です。これには、単純な比較だけでなく、増加率や減少率の計算も含まれることがあります。
例題
企業の年間売上比較
次の表は、A社とB社の年間売上(億円)を示しています。
2021年のA社の売上は2020年に比べて何%増加しましたか?

選択肢:
A. 5%
B. 10%
C. 20%
D. 25%
解説を詳しく見る
この解説では、A社の売上の増加率を計算する方法を示しています。2021年の売上から2020年の売上を差し引き、その結果を2020年の売上で割っています。具体的には、2021年の売上220億円から2020年の売上200億円を引き、その差を2020年の売上200億円で割り、最終的に100をかけています。この計算により、A社の売上が2020年に比べて2021年に10%増加したことがわかります。このような計算は、時間をまたいだデータの増減を分析する際に役立ち、ビジネスや経済の分野でよく用いられる基本的な手法です。
複数の表やグラフの関連性の例題
二つ以上の表やグラフが与えられ、それらがどのように関連しているかを理解し、情報を統合する能力が問われます。例えば、ある表が人数を示し、もう一つの表が割合を示している場合、これらの表のデータを関連付けて解答を導き出す必要があります。
例題
人口と公園数
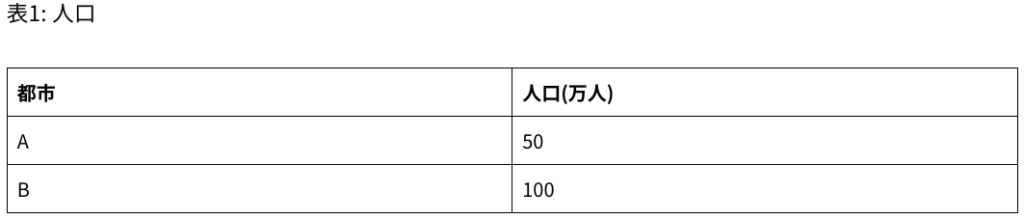
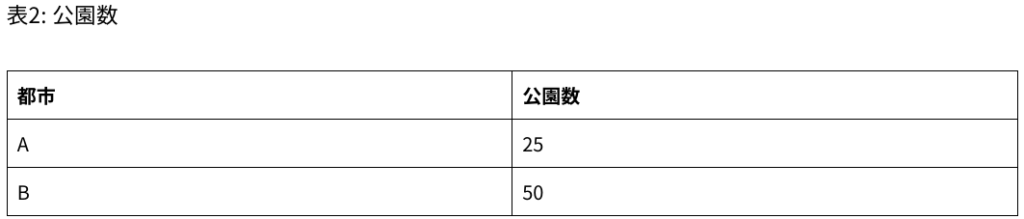
表1は都市AとBの人口を示し、表2は各都市の公園数を示しています。
都市Bの人口1万人あたりの公園数は、都市Aと比べて何倍ですか?
解説を詳しく見る
この問題の解説では、都市AとBの人口に対する公園数の割合を比較しています。都市Aの人口1万人あたりの公園数は0.5(25公園 ÷ 50万人)、都市Bも同様に0.5(50公園 ÷ 100万人)。これにより、両都市の人口あたりの公園数の割合が同じであることがわかります。この問題では、異なるデータセットからの情報を比較し、割合の計算を行うことで、2つの都市の公園の利用可能性を評価しています。このような分析は、データの解釈や比較を行う際の基本的なアプローチです。
特定条件下でのデータの解釈の例題
問題文に特定の条件が示され、その条件に基づいて表やグラフから正しい情報を読み取る必要があります。これには、条件によって変化する数値の解釈や、特定の条件下でのみ成り立つ数値関係の理解が含まれます。
例題
割引セールの効果
ある店舗で行われた1週間の割引セール中のデータです。割引前の通常価格と割引セール価格が以下のようになっています。
通常価格
・商品A: 1000円
・商品B: 2000円
割引セール価格
・商品A: 800円
・商品B: 1500円
セール期間中、商品AとBの売上合計は通常時の1.5倍になりました。このとき、セール期間中の商品Aと商品Bの販売数の合計は通常時の何倍になりましたか?
選択肢:
A. 1.2倍
B. 1.5倍
C. 2倍
D. 2.5倍
解説を詳しく見る
この問題では、特定の条件下(割引セール中)のデータ(商品価格と売上)を解釈する能力が試されます。セール期間中に商品AとBの売上合計が通常時の1.5倍になったことから、割引により価格が下がったにもかかわらず、売上の増加率が価格の割引率を上回ったことが示唆されます。これにより、販売数もそれに応じて増加したと考えられます。売上の増加率が1.5倍であるため、販売数も同様に1.5倍になったと推定できます。このように、異なるデータ間の関係性を理解し、それに基づいて論理的に結論を導くことが重要です。
対策のポイント
グラフや資料の読み取りには、データの正確な把握と分析が鍵となります。問題文を注意深く読み、必要な情報を正確に抽出することが重要です。また、データの比較や割合の計算などの基本的な数学スキルも役立ちます。さらに、問題文に隠されたヒントや条件を見逃さないようにすることが、効果的な対策につながります。
問題で与えられている情報を整理する
SPIのグラフ・資料の読み取り問題に取り組む際、問題文から提供される情報を整理することは極めて重要です。このプロセスは、問題解決のための基礎を築くことに他なりません。情報の整理には、まず問題文を慎重に読み、重要なデータやキーワード、条件を特定することが含まれます。例えば、距離、時間、速度、数値などが該当します。次に、これらの情報を視覚的に整理し、問題の構造を理解しやすくするために、図表やリストを作成します。さらに、情報の関連性を把握し、それを問題解決のための論理的な推論に結びつけます。また、問題文に与えられた条件下でどのように情報を適用するかを考え、解答に至るプロセスを構築します。この段階での情報の正確な整理は、後続の計算や分析の精度を高め、効率的な問題解決へと導く鍵となります。したがって、情報を整理する際には、丁寧かつ慎重に取り組むことが推奨されます。
整理の仕方を工夫する
SPIのグラフ・資料の読み取り問題において、情報の整理方法を工夫することは、問題解決への効果的なアプローチを形成する上で重要です。まず、問題文を読み、関連するデータを抽出します。次に、データを視覚的に整理し、理解を深めることがカギです。例えば、図や表を描く、情報をタイムラインに沿って配置する、重要なデータに色をつけるなどの方法が有効です。これにより、データ間の関係性が明確になり、論理的な思考が促進されます。
また、情報をカテゴリー別に分類することも役立ちます。例えば、数値データ、時系列データ、地理的データなどに分けて考えることで、問題の異なる側面を明確に理解することができます。さらに、問題解決に必要な情報とそうでない情報を区別し、重要な情報に焦点を当てることも重要です。この整理プロセスは、問題文に含まれる情報の複雑さを軽減し、より効率的に問題に取り組むための基盤を築きます。
尚、整理した情報を基にして、問題の解決策を段階的に構築します。情報を整理する際には、その情報が問題解決のプロセスにどのように貢献するかを常に考慮することが重要です。こうすることで、情報の整理は単なる前準備から、効果的な問題解決戦略へと変貌します。
求めるべきものが何かを理解する
SPIのグラフ・資料の読み取り問題では、何を求められているのかを正確に理解することが重要です。問題の核心に迫るためには、まず問題文を慎重に読み、問いの主旨を正確に把握する必要があります。これには、問題文中のキーワードや特定の数値、条件に注意を払うことが含まれます。例えば、問題文に「最も効率的な」というフレーズがあれば、最大や最小を求める問題である可能性が高いです。また、グラフや表から得られる情報と問題文が求めている内容を結びつけ、どの情報が解答に直接影響するかを特定します。例えば、特定の年の売上を求める問題では、その年に関連するデータに焦点を合わせる必要があります。問題解決の過程で、問題文が与えている条件や制限を考慮に入れ、それらが解答にどのように影響するかを検討することも重要です。このように、問題が具体的に何を求めているのかを正確に理解し、それに基づいた論理的な推論を行うことが、効果的な問題解決への鍵となります。
例題を解く
表の読み取り011
以下はA国とB国の発電方法に関する割合を1995年と2020年で比較した表である。
A国の1995年の発電量は6,100億kWhで、2020年の発電量は7,200億kWhである。
B国の1995年の発電量は7,500億kWhで、2020年の発電量は7,650億kWhである。
水力は再生可能エネルギーに含まれる。
A国の1995年の再生可能エネルギーの全体に占める割合は、22.4%であったが、2020年には34.9%にまで増えている。B国は1995年の9.3%から2020年には28.0%にまで増えた。
A国とB国の動向に関して正しく分析された内容を次の選択肢から一つだけ選べ。
例題:
A. A国の再生可能エネルギーからの発電量は1995年から2020年にかけ2倍以上に増え、B国の再生可能エネルギーからの発電量は1995年から2020年にかけて3倍以上に増えた。
B. B国の再生可能エネルギーからの発電量の25年間の変化量は A国の再生可能エネルギーからの発電量の25年間の変化量の1.25倍以上である。
C.B国の再生可能エネルギーからの発電量はこの25年間に3倍以上に増えたことで、A国よりも多く再生可能エネルギーを利用した発電が行われるようになった。
D.A国、B国ともに再生可能エネルギーからの発電量の割合は1995年には原子力からの割合よりも低かったが、両国ともに、2020年には再生可能エネルギーからの発電の方が多くの割合を占めるようになった。
解説を詳しく見る
A国の1995年の再生可能エネルギーからの発電量は6,100 × 0.224 = 1366.4(億kWh)
A国の2020年の再生可能エネルギーからの発電量は7,200 ×0.349 = 2512.8(億kWh)
2512.8 - 1366.4 = 1146.4 (億kWh)増えている。
これは割合に直すと約84%の増加である。
B国の1995年の再生可能エネルギーからの発電量は7,500 × 0.093 = 697.5(億kWh)
B国の2020年の再生可能エネルギーからの発電量は7,650 ×0.28 = 2142(億kWh)
2142-697.5=1444.5(億kWh)増えている。
これは割合に直すと3倍以上、約207%の増加である。
正しい記述は選択肢のうちBだけである。
表の読み取り010
以下はA国とB国の発電方法に関する割合を1995年と2020年で比較した表である。
A国の1995年の発電量は6,100億kWhで、2020年の発電量は7,200億kWhである。
B国の1995年の発電量は7,500億kWhで、2020年の発電量は7,650億kWhである。
水力は再生可能エネルギーに含まれる。
A国の1995年の再生可能エネルギーの全体に占める割合は、22.4%であったが、2020年には34.9%にまで増えている。発電量で比較した場合、1995年から2020年までにどれだけ変化しているか。以下の選択肢から正しい記述を一つだけ選べ。
例題:
A. 1,000億kWh以上増えている。
B. 1,200億kWh以上増えている。
C.2倍以上に増えた。
D.増加率は184%である。
解説を詳しく見る
A国の1995年の再生可能エネルギーからの発電量は6,100 × 0.224 = 1366.4(億kWh)
A国の2020年の再生可能エネルギーからの発電量は7,200 ×0.349 = 2512.8(億kWh)
2512.8 ÷ 1366.4 = 1.838 である。
したがって約84%の増加であるため、選択肢のうち正しい記述はAだけである。















