-
ホーム
-
SPI非言語
-
推論
SPIの「推論」の特徴
SPIの非言語分野の一つである「推論」では、与えられた情報を元に正しい答えを導き出す問題です。
この単元では、情報処理能力や論理的な思考が求められます。
推論の問題
それでは、推論とはどのような問題なのか。
例題と解説をみてみましょう。
例題
X、Y、Z、V、Wの5チームがサッカーのリーグ戦をおこなった。結果について以下のことがわかった。
Ⅰ YはXにだけ勝った。
Ⅱ Vは1勝3敗であった。
Ⅲ ZはXに勝った
すべての勝敗が確定をするためには、Ⅰ〜Ⅲとは別に、次のア、イ、ウのうち最低限どれが加わればよいか。AからHで1つ選びなさい。なお、引き分けはないものとする。
ア Xは2勝2敗であった。
イ 全勝のチームはいなかった。
ウ WはZに勝った。
選択肢:
A. アだけ
B. イだけ
C. ウだけ
D. アとイ
E. アとウ
F. イとウ
G. アとイとウ
H. 正しい推論はない
解説を詳しく見る
IからIIIを踏まえた状況を示した以下の勝ち負け表を参照する。

ア Xは2勝2敗であった。 ←①は確定するが、②は確定しない。
イ 全勝のチームはいなかった。←②が確定(WがZに勝った)し、①も確定(XがWに勝った)する。
ウ WはZに勝った。←②は確定するが①は確定しない。
したがってイだけ判明すれば、全勝敗が確定するため、正解はBとなる。
例題
X、Y、Z、Wの4人がテニスのリーグ戦をおこなった。勝敗について以下のことがわかっている。
Ⅰ XはZだけに勝った
Ⅱ YはWに勝った
必ず正しいといえる推論はどれか。AからHで1つ選びなさい。ただし、引き分けはないものとする。
ア Yが全勝なら、Zは1勝2敗
イ Zが2勝1敗なら、Yも2勝1敗
ウ Zが全敗なら、Wは2勝1敗
選択肢:
A. アだけ
B. イだけ
C. ウだけ
D. アとイ
E. アとウ
F. イとウ
G. アとイとウ
H. 正しい推論はない
解説を詳しく見る
IからIIを踏まえた状況を示した、以下の勝ち負け表を参照する。
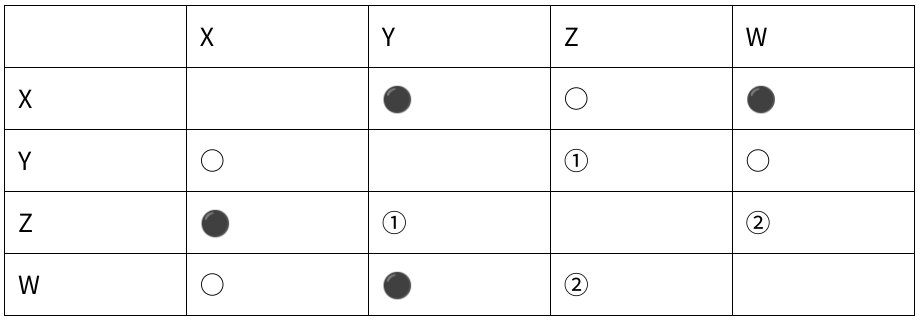
ア Yが全勝なら、Zは1勝2敗←①は確定するが、②は確定しないので誤り。
イ Zが2勝1敗なら、Yも2勝1敗←①と②が確定し、またその結果は正しいので正。
ウ Zが全敗なら、Wは2勝1敗←①と②が確定し、またその結果は正しいので正。
よって正しい推論はイとウなので、Fが答えとなる
対策のポイント
「推論」の対策ポイントを解説していきます。
繰り返し演習を行い問題に慣れることが重要となりますが、その際に下記のようなコツを意識して取り組んでみてください。
いかに短い時間で正解を導き出すかが重要となります。
①情報を表や記号を用いて整理する
「推論」は、論理的な思考が求められますが、まずは与えられた情報を適切に整理し処理することが必要となります。
A〜Cチームのように対象が3つ程度であれば、頭の中で整理もできますが、A〜Eチームのように5つ以上になると複雑になってきますので、わかる情報から表や図で関係性を見える化してみましょう。
頭でわかっている場合でも確認として書き出すと、ケアレスミスを減らすことにも繋がります。
②逆説も考える
例題を例に挙げると見落としがちなのが、「ZはXに勝った」という条件に対して、「XはZに負けた」という点です。
条件にある内容は、表に書き込んだり、考えたりするのですが、逆説を見落としてしまうことで、正しい解答を導けないことがあります。
条件を整理する際に逆からも考えるよう意識してみてください。
③必要な情報を考える
条件をただ読み並べただけでは、簡単に答えを導き出せないのが「推論」の特徴です。
そこから、正解に向けて一つずつ可能性を絞っていく必要があります。
確実に決まる部分を埋めた後は、次にどんな条件があれば、この関係性が決まるのかを考えてみてください。
特定の条件がないことにより、成り立たないのであれば、それもまた選択肢を絞ることに繋がります。
不足している情報を選択する問題には特に重要となる要素です。
例題を解く
推論(位置関係)007
A、B、Cの3人が、円形に並んだ4つの席のいずれかに座っています。各自の座り方について、次のことが分かっています。
Ⅰ AとBは隣り合っている。
Ⅱ 数字の3番の席は空席です。
Cが座った可能性のある席の番号は何番か。答えよ。
例題:
A. 1
B. 2
C. 4
D. 1か2
E. 1か4
F. 2か4
解説を詳しく見る
問題によると、A、B、Cの3人が円形に並んだ4つの席のいずれかに座っており、以下の条件が与えられています。
Ⅰ. AとBは隣り合っている。
Ⅱ. 数字の3番の席は空席です。
この条件に基づいて、Cが座った可能性のある席の番号を考えます。
Cが2番の席に座る場合:AとBは隣り合っている必要があり、3番の席は空席であるため、AとBは2番と4番の席に座ることになります。そして、Cが2番の席に座ることができます
Cが4番の席に座る場合:AとBは隣り合っている必要があり、3番の席は空席であるため、AとBは4番と1番の席に座ることになります。そして、Cが4番の席に座ることができます。
したがって、Cが座った可能性のある席の番号は4番だけです。したがって、正解は選択肢C(4)です。
推論(位置関係)006
P,Q,R,Sの3人が、カウンターに向かって1列に並んだ5つの席に座っている。各自の座り方について次のことが分かっている。
Ⅰ 3番の席は空席であった。
Ⅱ PとRは隣同士だった。
III Qの右側には誰も座っていない。
IV Pの左側にRが座っている。
Pが座っているのは何番か。
解説を詳しく見る
IとIIの条件により、P,RとS,Qの2グループに分けて考えることができる。
IIIの条件により、Qは⑤であることがわかり、PとRは①か②のどちらかであることがわかる。IVの条件よりPは②。














